Гиперсвязи с ограничениями на многообразии: визуализация проекции Синкхорна-Кноппа в 3D
---
ОПИСАНИЕ
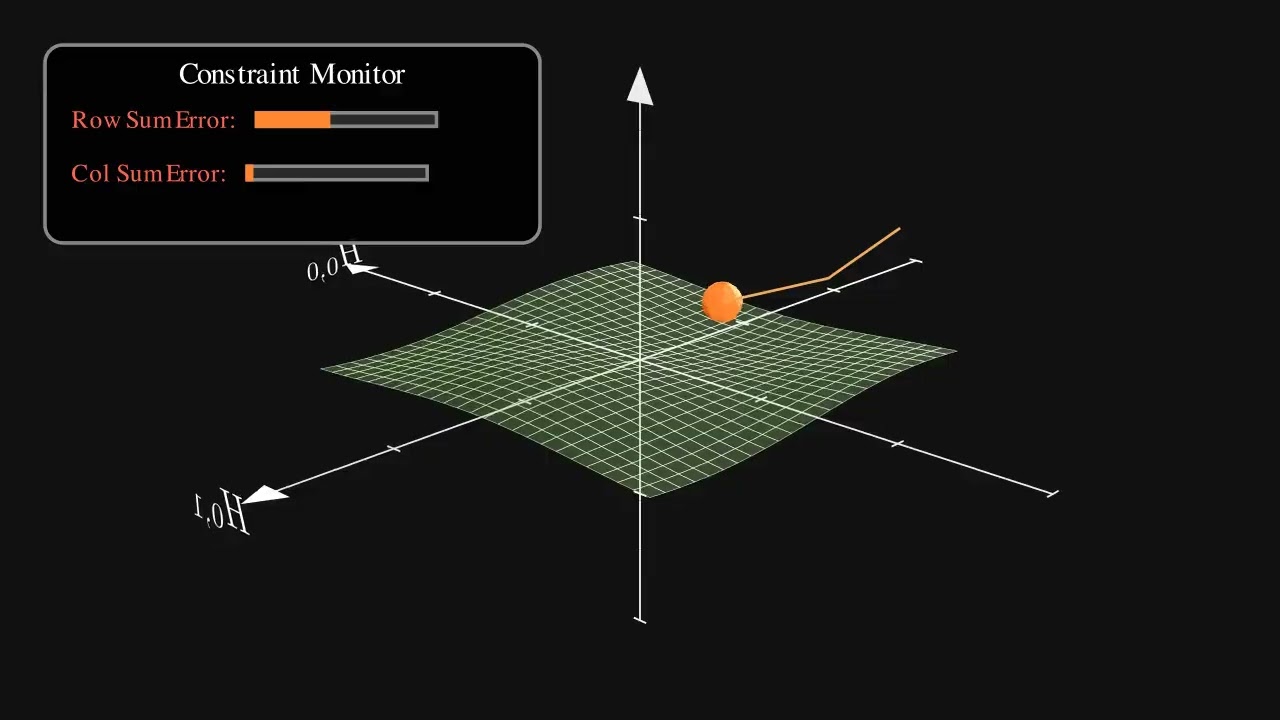
Узнайте, как алгоритм Синкхорна-Кноппа проецирует нестабильные веса нейронной сети на стабильное математическое многообразие. Эта 3D-визуализация оживляет абстрактную геометрию, лежащую в основе гиперсвязей с ограничениями на многообразиях (mHC), точно показывая, как удовлетворение ограничений предотвращает взрыв градиента в глубоком обучении.
Наблюдайте, как неограниченная матрица преобразуется посредством итеративной нормализации строк и столбцов, управляемой мониторингом ограничений в реальном времени, пока она идеально не окажется на многограннике Биркхофа — стабильной зоне, где сохраняется отображение идентичности.
---
РАЗДЕЛЫ
0:00 - Введение: Геометрия устойчивости
0:12 - Монитор ограничений: Понимание ошибок сумм строк и столбцов
0:24 - Первая проекция: Нормализация строк
0:32 - Вторая проекция: Нормализация столбцов
0:40 - Сходимость: Зигзагообразный путь к многообразию
0:48 - Успех: Ограничения выполнены и отображение тождественности восстановлено
---
КЛЮЧЕВЫЕ РАССМОТРЕНЫЕ ПОНЯТИЯ
• Математическое многообразие
Многогранник Биркхофа как поверхность ограничений
Зона устойчивости для весов нейронных сетей
Сохранение отображения тождественности
• Алгоритм Синкхорна-Кноппа
Чередующаяся нормализация строк и столбцов
Итеративный метод проекции
Сходимость к дважды стохастической матрице
• Мониторинг ограничений
Визуализация ошибки сумм строк
Ошибка сумм столбцов Отслеживание
Обратная связь по удовлетворению ограничений в реальном времени
• Стабильность гиперсоединений
Почему веса без ограничений резко возрастают
Как ограничения многообразия предотвращают нестабильность
Стабильность обучения в масштабе
---
МАТЕМАТИЧЕСКИЕ ОСНОВЫ
Многообразие ограничений определяется следующим образом:
• Ограничение по строкам: 1^T H_res = 1^T
• Ограничение по столбцам: H_res 1 = 1
Где H_res — матрица смешивания остатков в архитектуре гиперсоединений.
Алгоритм Синкхорна-Кноппа итеративно проецирует любую матрицу на это многообразие посредством:
1. Нормализации строк: H ← H / (H_суммы_строк)
2. Нормализации столбцов: H ← H / (H_суммы_столбцов)
3. Повторять до сходимости
---
ЦЕЛЕВАЯ АУДИТОРИЯ
• Исследователи машинного обучения, изучающие стабильность нейронных сетей
• Инженеры глубокого обучения, работающие с архитектурами трансформеров
• Студенты-математики, интересующиеся оптимизацией и многообразиями
• Специалисты по ИИ, внедряющие гиперсвязи
• Все, кто интересуется геометрией современных систем ИИ
---
ДЕТАЛИ ПРОИЗВОДСТВА
• Анимация: Manim (3D математическая визуализация)
• Визуальный стиль: Темная тема с цветовой кодировкой ограничений
• Аудио: Профессиональное повествование, синхронизированное с визуальными подсказками
• Продолжительность: 1 минута 10 секунд
• Качество: 720p30
---
ОСНОВНЫЕ ВЫВОДЫ
1. Веса нейронной сети должны удовлетворять ограничениям, чтобы предотвратить нестабильность.
2. Алгоритм Синкхорна-Кноппа предоставляет элегантный метод проекции.
3. Мониторинг ограничений в реальном времени делает процесс прозрачным.
4. Ограничения многообразия сохраняют свойства отображения тождественности.
5. Эта техника обеспечивает стабильное обучение большого количества моделей.
---
СВЯЗАННЫЕ ТЕМЫ
#ГлубокоеОбучение #НейронныеСети #ОбучениеМногообразий #АлгоритмСинкхорна #Гиперсвязи #Оптимизация #ПроекцияМатрицы #ПолитопБиркхофа #УдовлетворениеОграничений #ГрадиентнаяСтабильность #АрхитектураТрансформаторов #МашинноеОбучение #ИскусственныйИскусственныйИнтеллект #МатематическаяВизуализация #3DAнимация
---
ТЕГИ
Гиперсвязи с ограничениями многообразия, mHC, Алгоритм Синкхорна-Кноппа, Политоп Биркхофа, Двойная стохастическая матрица, Удовлетворение ограничений, Стабильность нейронной сети, Предотвращение градиентных взрывов, тождественное отображение, нормализация матриц, ограничение суммы строк, ограничение суммы столбцов, 3D-визуализация, математическое многообразие, алгоритмы оптимизации, глубокое обучение, архитектура трансформера, ограничения весов, стабильность обучения
---
ПОДПИСЫВАЙТЕСЬ, чтобы увидеть больше визуализаций передовых концепций машинного обучения!

Информация по комментариям в разработке