Kd (equilibrium dissociation constant) & how binding assays let us find it

Kd (the equilibrium dissociation constant) is a measure of binding affinity & it’s the concentration of one binding partner at which half of the other binding partner is bound. But WHY? Where does that come from? Why should we care? Well, the relationship allows us to use binding assays (experiments), altering the concentration of one partner & measuring the fraction of the other partner bound in order to determine the Kd. Here’s how…

blog form (also has static graphics): http://bit.ly/kdaffinitytalk
⠀
We can measure binding affinity by altering the concentrations, measuring the binding, and fitting it to an equation that takes into account the contribution of concentration and “hides it” so you can see the constant part - the affinity! If that didn’t make sense, bear with me and I’ll get into more detail, but the end result is we get a value called the dissociation constant, abbreviated Kd. This value tells us what concentration of one binding partner (we can call it B if you want) would lead to half of its binding partner (we’ll call A) being bound at equilibrium (i.e. once the rates of binding and unbinding have stabilized and the mixture has found its happy ratio of bound & unbound). ⠀
⠀
The higher the affinity (the more sticky they are for one another) the less ligand is required to reach that value- higher affinity is like thinking the partner’s prince charming - you’ll take him whenever you find him - so lower Kd. But if you think there’s still someone better out there you might “hold off” unless there’s so many of that okay-ish match that you “give in” - so higher Kd.⠀
⠀
This is a really important, though potentially confusing, concept to remember:⠀
higher affinity → lower Kd⠀
lower affinity → higher Kd⠀
⠀
As an equilibrium constant (more on what this means in a second), Kd is a sort of “endpoint” measurement. ⠀
⠀
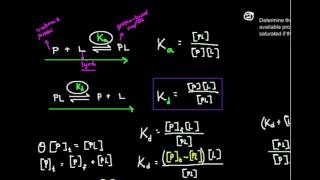
We have this situation of A + B ⇌ AB, and we can measure the concentrations of one or more of these, and we can denote “concentration of” with brackets, so the situation’s [A] + [B] ⇌ [AB] and when we measure Kd it’s like taking a molecular census of bound [AB] and unbound partners [A] & [B] after the binding & unbinding has stabilized. ⠀
⠀
So Kd is dependent on the rates of binding and unbinding (which are dependent on inherent properties of the molecules & how well they complement one another, as well as conditional things like temperature). ⠀

We can define Kd in terms of “rate constants” as Kd = koff/kon. In words this means that if you were to look at 2 binding partners, the concentration of one required to get half of the other bound is the chance of “unbinding” (koff) divided by the chance of binding (kon).⠀
⠀
When you get into talking about rates, you’ve entered the world of “kinetics” and you’ve gotta start measuring things over time. A lot of times, instead of studying kinetics, you turn to thermodynamics, which deals with measuring things at equilibrium. Instead of tracking them over time, we can take a single “census” after we give the molecules enough time to come to a dynamic equilibrium (rates of marriage & divorce are constant so there’s no net change even if the couples themselves are changing). The more you see that are “married” compared to single when you take the census, the greater the affinity between the two. And remember, in order to be legit, you’ve gotta take this census after you’ve given them enough time to reach equilibrium (a time that depends on the rate constants, with slow-offers taking longer to equilibrate. more on this here: https://elifesciences.org/articles/57264 )⠀
⠀⠀
Methods and binding partners vary but the basic gist of most equilibrium binding assays is you do a serial dilution (e.g. half then half of that then half of that) of A. You start with WAY more of A than the labeled B (even at your lowest concentration point) This way, when B binds A there’s still a ton of A left to bind. So in the whole [A] + [B] ⇌ [AB] scheme, when you take some protein out of commission by moving it to the right side, it’s like removing a drop from a bucket – so you can think of the concentration of free A as constant in each mix – A is Prince Charming, you don’t need to worry about copies of B “competing” for Prince Charmings. Instead, what you want is each A deciding for themselves whether to bind based on how much they like the Prince, not how many Princes there are.⠀
⠀
This is only true if the concentration of the labeled B is way below the Kd of the interaction. If the B concentration is too high, so much of the protein will get bound that it lowers the amount of free Princes in a meaningful way, so you get what’s called “ligand depletion” – to avoid this you want to stay at least 10x under the Kd. And you want the A concentration series to range from ~100-fold less – ~100-fold more than the B concentration
⠀
Plot out fraction B bound vs concentration and you can figure out the affinity. ⠀