Скачать или смотреть Key Properties of Regression You Never Knew |

Key Properties of Regression You Never Knew | @perfectcommercecoaching Regression analysis is used to model the relationship between a dependent variable (response) and one or more independent variables (predictors). Key properties include:

Linearity: Regression assumes a linear relationship between the dependent and independent variables in the simplest form (linear regression). The model predicts the dependent variable as a linear function of the independent variable(s).

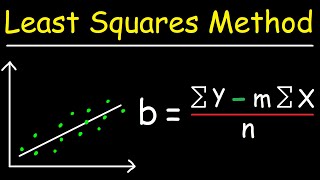
Least Squares Estimation: In linear regression, the model finds the best-fit line by minimizing the sum of squared residuals (differences between observed and predicted values).

Bias and Variance: A good regression model balances bias (error due to oversimplification of the model) and variance (error due to overfitting). Reducing one often increases the other.

Goodness of Fit (R²): This property indicates how well the regression line explains the variation in the dependent variable. It ranges from 0 (no explanation) to 1 (perfect fit).

Multicollinearity: When using multiple independent variables, high correlations between predictors can distort the model’s estimates, causing multicollinearity.

Homoscedasticity: Regression assumes constant variance of residuals across levels of the independent variables. This property is important for proper model estimates.

Independence of Errors: Errors (or residuals) should be independent, meaning the error for one observation should not be correlated with the error for another.

Normality of Errors: In linear regression, it is assumed that the errors follow a normal distribution. This is important for inference and hypothesis testing.

Regression Coefficients: The coefficients (slope and intercept in simple linear regression) represent the effect of each independent variable on the dependent variable.

Properties of Covariance:
Covariance measures how two random variables change together. It gives an indication of the direction of the linear relationship between variables.

Symmetry: Covariance between two variables
𝑋
X and
𝑌
Y is symmetric, i.e.,
Cov
(
𝑋
,
𝑌
)
=
Cov
(
𝑌
,
𝑋
)
Cov(X,Y)=Cov(Y,X).

Sign of Covariance:

Positive Covariance: If
𝑋
X and
𝑌
Y increase or decrease together, the covariance is positive.
Negative Covariance: If
𝑋
X increases while
𝑌
Y decreases, or vice versa, the covariance is negative.
Zero Covariance: If there is no linear relationship between
𝑋
X and
𝑌
Y, covariance will be zero.
Units of Measurement: Covariance depends on the units of the variables being measured. This makes it difficult to interpret the magnitude directly. For standardized interpretation, correlation (which normalizes covariance) is often preferred.

Linearity: Covariance is a linear operation, i.e.,
Cov
(
𝑎
𝑋
+
𝑏
,
𝑌
)
=
𝑎
⋅
Cov
(
𝑋
,
𝑌
)
Cov(aX+b,Y)=a⋅Cov(X,Y), where
𝑎
a and
𝑏
b are constants.

Invariant under Addition of a Constant: Adding a constant to one or both variables does not affect the covariance, i.e.,
Cov
(
𝑋
+
𝑐
,
𝑌
)
=
Cov
(
𝑋
,
𝑌
)
Cov(X+c,Y)=Cov(X,Y).

Affected by Scaling: Multiplying one variable by a constant scales the covariance by that constant, i.e.,
Cov
(
𝑎
𝑋
,
𝑌
linear regression,regression analysis,regression,coefficients of regression,lines of regression,slope of the regression line,multiple linear regression,principle of regression,regression equation,regression coefficients,regression in machine learning,linear regression machine learning,linear regression excel,regression line,multiple linear regression excel,linear regression solved example,@perfectcommercecoaching,linear regression analysis
)
=
𝑎
⋅
Cov
(
𝑋
,
𝑌
)
Cov(aX,Y)=a⋅Cov(X,Y).

Non-Directional: Covariance only indicates the direction of the relationship (positive or negative) but does not give specific details about the strength or form of the relationship.

Key Differences:
Regression gives a model for predicting one variable based on others, whereas covariance only measures the direction of the linear relationship.
Regression coefficients give information on the strength of the relationship, while covariance does not offer this insight.
Both are foundational in understanding relationships in data, with covariance being a building block for more advanced concepts like correlation and regression.