Скачать или смотреть Nonlinear Transformation Functions, Black Hole Inversion, Expanding Universe Flow, Galaxy Spirals

Follow LinkTree for App or copy and paste from here:
https://uuonmind.my.canva.site/nonlin...

#quantumphysics #blackholes #universe #mathematics #coding

Key Transform Functions:

1. \frac{1}{z}
• Inverts the plane: points near the origin get pushed far away, and far-away points collapse inward.
• Visual: like flipping the world inside-out, creating rings and mirrored folds.

2. z^2
• Squares every point: angles double, distances stretch.
• Visual: circles turn into ellipses, spirals tighten — patterns rotate twice as fast.

3. z^3
• Cubes the point: angles triple, distances expand even more.
• Visual: a kaleidoscope effect, with triple symmetry around the origin.

4. e^z (exponential)
• Turns straight lines into curves, maps the infinite plane into repeating wave-like strips.
• Visual: grids warp into flowing, river-like waves with repeating patterns.

5. \cos(z)
• Cosine waves in two directions (real & imaginary).
• Visual: rippling folds, spirals that look like galaxies or seashells.

6. \log(z)
• The opposite of exponential. Expands small distances and compresses large ones.
• Visual: spirals unwrap into layers, like peeling an infinite onion.

7. \sqrt{z}
• Square root halves angles: turns one full rotation into just half.
• Visual: the plane “splits” into mirrored sheets — a two-layered spiral effect.

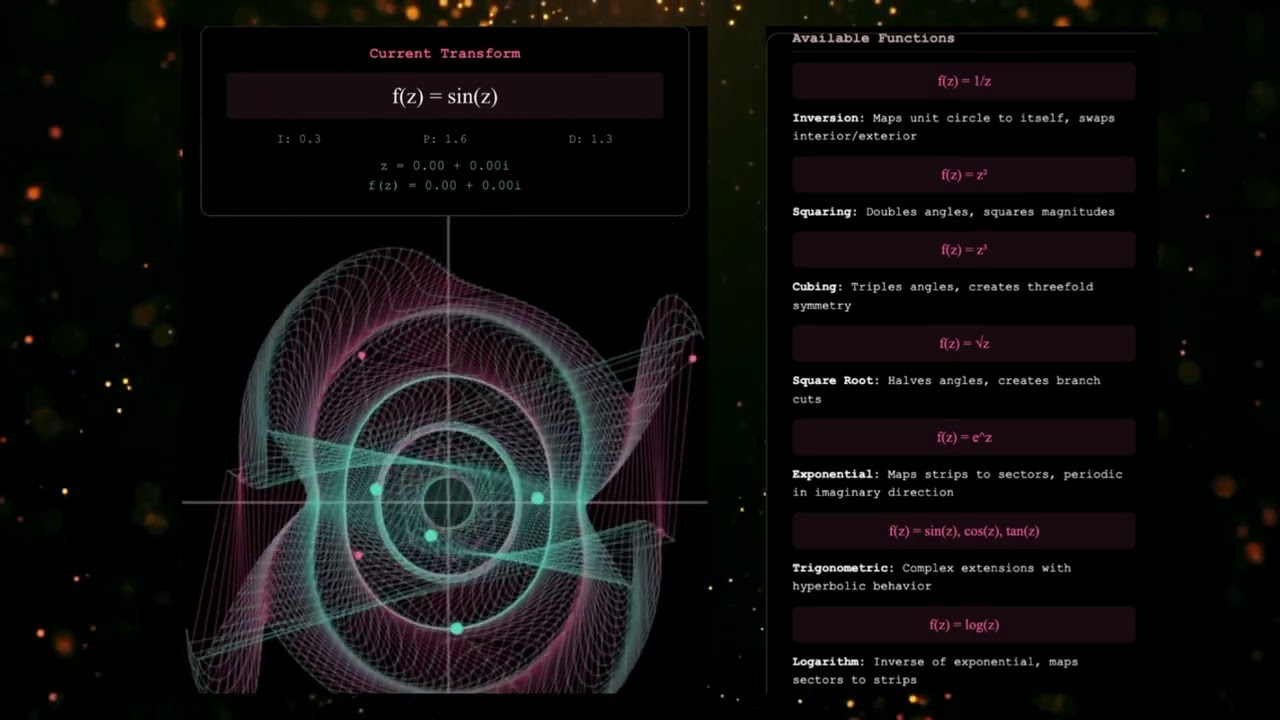
8. \sin(z)
• Sine wave across the complex plane, similar to cosine but shifted.
• Visual: smooth alternating ripples, often more symmetric than cosine.

9. \tan(z)
• Tangent = sine / cosine, so it creates repeating poles where values blow up.
• Visual: dense grid of sharp spikes and folds, infinite repeats.

10. z^n
• General power function: n controls symmetry and stretching.
• Visual: like z^2 or z^3, but adjustable — each value of n creates new rotational symmetries and folding patterns.


Cosmic Connections:
• 1/z: Black hole inversion.
• z^2, z^3, z^n: Galaxy spirals with rotational symmetry.
• e^z: Expanding universe flow.
• \cos(z), \sin(z): Wave interference like light or sound.
• \tan(z): Explosive starfields with singularities.
• \log(z): Layers of time unfolding.
• \sqrt{z}: Multiverse split into two sheets.

What this app does is show us that math is more than number, it’s a living language. Here, with the functions f(z) = \cos(z) and various others, we see how a simple equations can blossom into spirals and folds, almost like galaxies spinning in space. The sliders let us tune intensity, phase, and density, just like adjusting the focus of a telescope. Each adjustment reveals hidden patterns, as though we’re uncovering layers of reality itself.

This idea isn’t isolated, t’s part of a growing movement in science and design to reveal mathematics as a universal pattern-maker. Wolfram Demonstrations, for example, offers thousands of interactive explorations where equations turn into visuals we can play with. In physics, NASA and ESA use high-precision simulations to visualize galaxies, black holes, and cosmic microwave backgrounds, showing us how the universe evolves on scales we can’t observe directly.

In design and computation, projects with Three.js and WebGL take abstract formulas and transform them into immersive 3D structures, sometimes for art, sometimes for virtual reality, sometimes to model molecular or quantum systems. Even in neuroscience, researchers map brain networks using similar visual techniques, finding fractal patterns that echo the same geometry we see in the stars.

All of these efforts point to the same idea: the universe runs on hidden equations, and by turning those equations into living pictures, we can start to understand its language. The precision goes down to unimaginable decimals, yet when we look at it as shape and color, the complexity becomes something we can feel.

So this app is more than just visuals, it’s a window into the next level of mathematics, where art, science, and technology merge. By exploring these patterns, we’re not just watching equations, we’re watching the bones of the universe paint themselves before us, showing how everything, from seashell spirals to galaxies, might be part of one collective system, woven together by math.

© UUON Foundation, 2025, All Rights Reserved.