Комментарии на тему 1+2+3+...=-1/12 от запутавшихся людей, возникших благодаря печально известному видео на канале Numberphile, продолжают наводнять секции под моими и другими математическими видео на YouTube. Поэтому я решил, что пришло время сделать ещё одну серьёзную попытку расставить все точки над i и детально разобраться в тех странных вычислениях, что были в центре внимания в том видео на Numberphile. А именно, ясно и чётко сказать, что в них неверно, как это исправить и как связать их с истинной математикой, которую профессора на Numberphile имели в виду изначально.
Это моя вторая попытка по достоинству разобрать эту тему, на этот раз со стороны совсем другого подхода по сравнению с первым видео -- больше никаких недомолвок и ужимок, полный ва-банк. В результате получилось безумное видео длиной в целых 41.44 (почти 42 :) ) минуты.
Нас ждёт много замечательной математики: нестандартные методы суммирования расходящихся рядов, η-функция -- очень удобная для анализа сестра дзета-функции, а также самая суть аналитического продолжения простыми словами, и т.д.
Оригинальное видео на Numberphile можно найти здесь: • ASTOUNDING: 1 + 2 + 3 + 4 + 5 + ... =... . Также советую посмотреть другие видео и записи, на которые приведены ссылки в описании к тому видео.
Вот ссылка на личную тетрадь Рамануджана (Ramanujan), которая содержит вычисления касательно 1+2+3+... = -1/12, похожие на выкладки в видео Numberphile. http://www.imsc.res.in/~rao/ramanujan...
Эта запись в его тетради была одной из отправных точек моего последнего видео на эту тему: • Ramanujan: Making sense of 1+2+3+... ...
Другие хорошие видео, которые имеют дело с этим странным "тождеством", включают в себя:
• Why -1/12 is a gold nugget (видео на Numberphile с участием математика Эдварда Френкеля (Edward Frenkel), который тоже говорит о связи между дзета-функцией Римана и безумным тождеством Рамануджана.)
• But what is the Riemann zeta function... (отличное видео канала 3Blue1Brown о визуализации аналитического продолжения дзета-функции Римана)
Если вы знаете немного матанализа и хотите продолжить читать об этой теме, помимо того, что доступно на соответствующих страницах Википедии и других интернет-ресурсах, я бы порекомендовал прочитать последнюю главу книги за авторством Конрада Кноппа (Konrad Knopp) "Theory and applications of infinite series", Dover books, 1990 (а если вы ещё и знаете немецкий, прочитайте расширенную версию этой главы в оригинальном выпуске этой книги 1924 года).
Обычно люди ещё советуют книгу Харди (G.H. Hardy) "Divergent series", но я бы сказал, что её стоит читать только после прочтения главы из книги Кноппа; она куда более доступна, на мой взгляд. Несмотря на это, в книге Харди присутствует много интересных деталей о том, как суммирование по Рамануджану применяется к дзета-функции; см. главы 13.10 и 13.17.
Статья за авторством Терри Тао (Terry Tao), которую я упомянул в видео, живёт по вот этому адресу: https://terrytao.wordpress.com/2010/0...
Спасибо большое моему другу, математику Марти Россу, за его помощь и комментарии по поводу сценария к этому видео, и за придирчивый голос на заднем плане; а также Данилу Дмитриеву, официальному русскому переводчику канала Mathologer, за его субтитры.
Наслаждайтесь :)
Буркхард (Burkard)
P.S. Тут вы найдёте скан той страницы из книги по теории струн, которая демонстрируется в видео на Numberphile. В частности, обратите внимание на использование знаков равенства и стрелок на этой странице. http://www.qedcat.com/misc/String_the...
Сегодняшние математические футболки могут быть найдены при помощи поиска в гугле:
"zombie addition math t-shirt" (англ. "прибавление зомби математическая футболка"),
"label your axes math t-shirt" (англ. "всегда обозначайте свои оси", axes = "оси", "топоры").



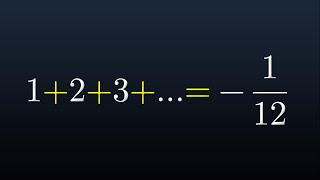


![Как считали число пи? [Veritasium]](https://i.ytimg.com/vi/A3PL61fHzjs/mqdefault.jpg)


![The most beautiful equation in math, explained visually [Euler’s Formula]](https://i.ytimg.com/vi/f8CXG7dS-D0/mqdefault.jpg)
Информация по комментариям в разработке