Скачать или смотреть AI finds a quantum error correcting code for bit flip errors (3 logical and 4 physical qubits)

This is a visualization of an AI finding a quantum error correcting code during the process of training.

Suppose that U,V,W are complex Euclidean spaces. Let N denote a quantum channel from V to W. Then the goal is to find quantum channels D,E where
the Frobenius norm of ||DNE-I|| is minimized and where E takes U to V and D takes W to U. We minimize the Frobenius norm using gradient descent. We restrict the domain of the loss function to pairs (D,E) where D,E have Choi rank at most 3, and we set dim(U)=8. We also restrict the loss function to the case where D,E are real quantum channels instead of complex quantum channels.

In our case, we have V=W with dim(V)=dim(W)=16. The channel N selects one of the four qubits and with 1/2 probability performs a bit flip operation on one of the four qubits.

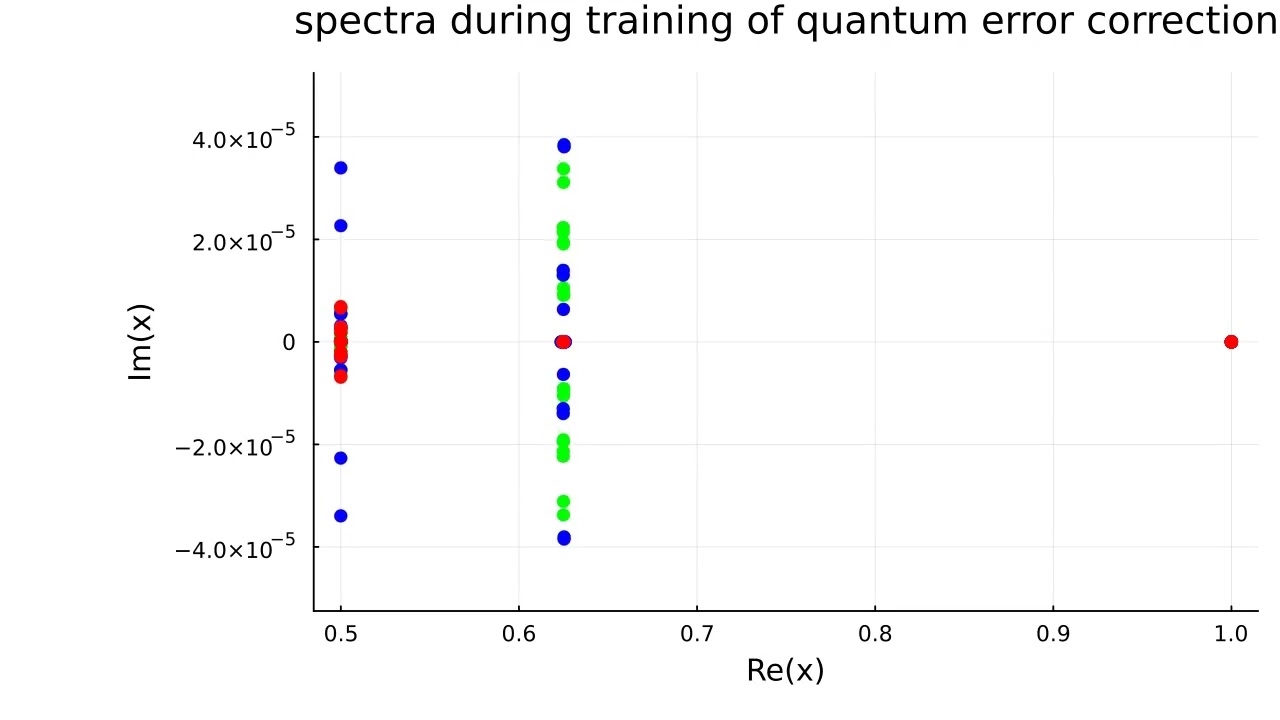
For the visualization, we locally minimize the loss level three times using gradient descent, and we use a different color (red,green,blue) for each time that we locally minimize this loss level. In the visualization, we show the spectrum of the operator DNE during training for all three instances, but we pop off the dominant eigenvalue 1 since the dominant eigenvalue is too far away from the other eigenvalues during training. For a smooth visualization, we begin with a low loss level at the beginning of training and we gradually increase the loss level up and we use an adaptive learning rate to control the loss level so that we do not reach instability. In our case, we see some instabilities in the visualization as the adaptive learning rate algorithm takes several iterations of gradient descent to reduce the learning rate to a stable level.

The notions of gradient descent and of quantum error correction are not my own, but I have slightly modified the notion of quantum error correction in a few ways. Here, instead of requiring the quantum error correcting code (D,E) to perfectly correct errors so that DNE is the identity channel, we only require that the code (D,E) minimizes the amount of error in the loss. Here, I allow the Choi rank of D,E to be 8 which is a bit overkill for the encoding channel since after training, the encoding channel E has Choi rank 1. Instead of letting D,E be general complex matrices, we set D,E to simply be real matrices.

There are a few things going on in this visualization. We see that after training, the error correcting code (D,E) behaves mathematically and is quite interpretable. In each of the training instances, we obtain the same spectra after training. After training, all the eigenvalues of DNE are real and have values 1/2,5/8,1 with multiplicity. The interpretability of (D,E) tells us that not only is the noise channel N an object that can be studied mathematically, but our loss function is also a loss function that can be studied mathematically and will produce interpretable results. We also observe that even though quantum channels are typically defined as superoperators between complex Euclidean spaces, in our case, we restrict our attention to functions of a real variable and everything works out well.

Unless otherwise stated, all algorithms featured on this channel are my own. You can go to https://github.com/sponsors/jvanname to support my research on machine learning algorithms. I am also available to consult on the use of safe and interpretable AI for your business. I am designing machine learning algorithms for AI safety such as LSRDRs. In particular, my algorithms are designed to be more predictable and understandable to humans than other machine learning algorithms, and my algorithms can be used to interpret more complex AI systems such as neural networks. With more understandable AI, we can ensure that AI systems will be used responsibly and that we will avoid catastrophic AI scenarios. There is currently nobody else who is working on LSRDRs, so your support will ensure a unique approach to AI safety.