How to do the series convergence tests for your Calculus 2 class. You will learn all types of convergence tests including direct comparison, telescoping series, limit comparison test, ratio test, root test, p-series, geometric series, and more! Best wishes for your calculus 2 class!
Get a Convergence t-shirt: 👉 https://www.amazon.com/dp/B0C54H5TZV
Try the problems first: 👉 / files-to-my-100-95153770
Check out my other "100-everything" series:
100 Derivatives: • 100 calculus derivatives (ultimate de...
100 Integrals: • 100 integrals (world record?)
100 Series: • 100 series convergence tests (no food...
100 Calculus 2 Problems: • 100 calculus 2 problems! (ultimate fi...
mistakes
Thanks to several viewers, at Q25, 1:53:40 , n should go from "2" to inf. And in that case, cos(pi*n) will produce 1,-1,1,-1,... but it is still a convergent alternating series.
Thanks to Chester, at 2:34:35, I meant to say 1/3 is less than "1", not 0. So we can draw a conclusion from the Ratio Test.
Thanks to Alberto! At 4:52:58 the final answer should be x is less than “-1”
Highlights: (see pinned comment for ALL timestamps)
start: 0:00
1, Classic proof that the series of 1/n diverges, 4:17
2, series of 1/ln(n) by The List, 11:10
3, series of 1/(ln(n^n)) by Integral Test, 17:05
4, Sum of 1/(ln(n))^ln(n) by Direct Comparison Test, 22:45
9, Sum of (-1)^n/sqrt(n+1) by Alternating Series Test, 49:10
15, Sum of n^n/(n!)^2 by Ratio Test, 1:22:20
16, Sum of n*sin(1/n) by Test for Divergence from The Limit, 1:28:04
26, Sum of (2n+1)^n/n^(2n) by Root Test, 1:58:11
30, Sum of n/2^n, 2:10:40
32, Sum of 1/n^(1+1/n), 2:22:30
41 to 49, true/false: 2:52:58
90, Sum of (-1)^n/n! = 1/e by Power Series, 5:24:40
100, Alternating Harmonic Series 1-1/2+1/3-1/4+1/5-... converges to ln(2) by Power Series, 5:54:40
101, Series of 3^n*n!/n^n by Ratio Test, 6:00:00
#100series #calculus #satisfying #apcalculus #gcse
May 6th, 2019







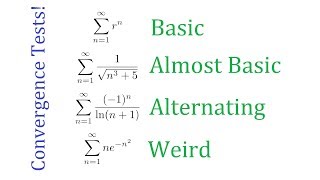


Информация по комментариям в разработке