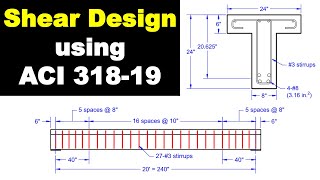
Shear Capacity of Reinforced Concrete Beams using ACI 318-19
Скачать Shear Capacity of Reinforced Concrete Beams using ACI 318-19 бесплатно в качестве 4к (2к / 1080p)
У нас вы можете скачать бесплатно Shear Capacity of Reinforced Concrete Beams using ACI 318-19 или посмотреть видео с ютуба в максимальном доступном качестве.
Для скачивания выберите вариант из формы ниже:
Cкачать музыку Shear Capacity of Reinforced Concrete Beams using ACI 318-19 бесплатно в формате MP3:
Если иконки загрузки не отобразились, ПОЖАЛУЙСТА,
НАЖМИТЕ ЗДЕСЬ или обновите страницу
Если у вас возникли трудности с загрузкой, пожалуйста, свяжитесь с нами по контактам, указанным
в нижней части страницы.
Спасибо за использование сервиса video2dn.com









Информация по комментариям в разработке