Deriving the mean and variance of the least squares slope estimator in simple linear regression
Скачать Deriving the mean and variance of the least squares slope estimator in simple linear regression бесплатно в качестве 4к (2к / 1080p)
У нас вы можете скачать бесплатно Deriving the mean and variance of the least squares slope estimator in simple linear regression или посмотреть видео с ютуба в максимальном доступном качестве.
Для скачивания выберите вариант из формы ниже:
Cкачать музыку Deriving the mean and variance of the least squares slope estimator in simple linear regression бесплатно в формате MP3:
Если иконки загрузки не отобразились, ПОЖАЛУЙСТА,
НАЖМИТЕ ЗДЕСЬ или обновите страницу
Если у вас возникли трудности с загрузкой, пожалуйста, свяжитесь с нами по контактам, указанным
в нижней части страницы.
Спасибо за использование сервиса video2dn.com
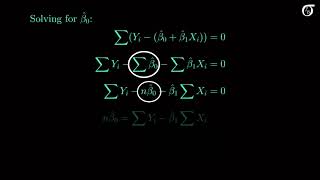








Информация по комментариям в разработке