PID controllers are popular control mechanisms found in many systems used to help drive the main process’s output to achieve some desired set point. PID stands for “proportional, integral, derivative.” The controller compares the output of the process to some set point to create an error term. That error term is used in three separate calculations to produce a control signal for the process or plant.
The written description for PID controllers can be found here: https://www.digikey.com/en/maker/proj...
In the video, we use an example of a cruise control system in a car. We want to design a mechanism that can maintain a constant speed by controlling the position of the accelerator (gas pedal). PID controllers are a perfect fit for such a system. In fact, most modern cars use PID controllers for cruise control.
A simple, naive approach to designing such a controller is to adjust the process’s input signal based on the set point alone with no feedback. This is known as an “open-loop control system.” This may work in some cases, but most of the time, the output is dependent on other factors (such as road conditions and hill climbs for our cruise control system). As a result, we need to incorporate feedback into our controller.
A “closed-loop control system” measures the actual output of the process and compares it to the set point. The error is the difference between these two values, and it’s used as the input to the controller. The controller looks at that error and makes adjustments as needed to the process’s input.
The proportional (P) part of the PID controller simply multiplies the error term by a constant, Kp. The further away the process’s output is from the set point, the higher the magnitude of the input value. This works in some cases, but it can result in “steady-state error” where the desired output can never be achieved. In our cruise control example, if we are at our cruising speed, the error is 0, which means that we should completely release the gas pedal. Obviously, this is not a desired behavior, so we add additional terms to our controller.
The integral (I) term sums the error term over time and multiplies this sum by a constant, Ki. This process solves the issue of steady-state error found in the P controller. As the steady-state error accumulates, the I term causes the process input signal to increase, thus closing the gap found in that steady-state error. It essentially looks at the past performance of the system and adjusts as needed.
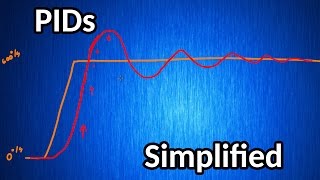
Sometimes, a PI controller is sufficient. However, you often face a tradeoff when tuning such a system. You can either have an “overdamped response” where the error slowly (but surely) approaches 0, or you can have an “underdamped response” in which the output quickly approaches the set point but oscillates for some time. If you want a “critically damped” system that quickly approaches the set point and settles with little or no oscillation, you need to add a third term.
The derivative (D) term counteracts the effects of the proportional and integral terms. It attempts to predict where the response is headed by solving for the slope of the error curve and multiplying that value by the constant Kd. If the magnitude of the slope is too high, such that the system is approaching 0 error too quickly, it will add a negative value to the sum of the P and I terms, thus “pulling back” on the input.
With properly tuned Kp, Ki, and Kd values, systems should ideally become critically damped where the output quickly approaches the set point without any overshoot. Tuning a PID controller can be quite involved, and we will cover it in a future video.
Note that most modern PID controllers are implemented in software to run on computers or microcontrollers. We provide a snippet of pseudocode to help you get started implementing your own PID controllers in, say, Arduino.
Product Links:
STMicroelectronics Inverted Pendulum Kit - https://www.digikey.com/en/products/d...
Related Articles:
STMicroelectronics Inverted Pendulum Kit Curriculum - https://www.st.com/content/st_com/en/...
Learn more:
Maker.io - https://www.digikey.com/en/maker
DigiKey’s Blog – TheCircuit https://www.digikey.com/en/blog
Connect with DigiKey on Facebook / digikey.electronics
And follow us on Twitter / digikey
00:00 - Intro
00:57 - Control Theory Overview
02:53 - Open-loop System
03:59 - Closed-loop System
05:06 - Proportional Controller - Distance
07:37 - Proportional Controller - Cruise Control
10:04 - Proportional and Integral Controller
14:05 - Over, Under, and Critically Damped Responses
15:04 - Proportional, Integral, and Derivative Controller
18:12 - PID Controller Tuning
19:43 - Code Example
21:09 - Use Cases
21:44 - Conclusion







![Как устроены швейные машинки? [Veritasium]](https://i.ytimg.com/vi/FFW0GcMCgd0/mqdefault.jpg)
Информация по комментариям в разработке