In this four-part series we explore propositional logic, Karnaugh maps, implications and fallacies, predicate logic, existential and universal quantifiers and finally natural deduction.
Become a member: https://youtube.com/Bisqwit/join
My links:
Twitter: / realbisqwit
Liberapay: https://liberapay.com/Bisqwit
Patreon: / bisqwit (Other options at https://bisqwit.iki.fi/donate.html)
Twitch: / realbisqwit
Homepage: https://iki.fi/bisqwit/
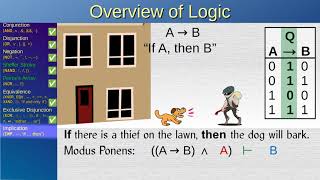
Summary of the introduction and elimination rules. Here [M]→N means that by temporarily assuming that M is true you can conclude N. If N is already true, you can just use N directly and ignore M. If you already know M is true (for example it is a premise), you should not mark it temporary. “Is valid” means that you can make that conclusion. “Is true” means that the expression has already been concluded or given as a premise.
INTRODUCTION RULES:
I Conjunction/AND:
If P and Q, then P∧Q is valid.
I Disjunction/OR:
If P, then P∨Q is valid.
If Q, then P∨Q is valid.
I Biconditional/equivalence (↔):
If [P]→Q and [Q]→P, then P↔Q is valid.
I Implication (→):
If [P]→Q, then P→Q is valid.
I Negation (NOT):
If [P]→(Q∧¬Q), then ¬P is valid.
I Universal quantifier (∀):
If P is true independent of x, then ∀xP is valid.
I Existential quantifier (∃):
If P(y), then ∃xP(x) is valid for some independent variable x.
ELIMINATION RULES:
E Conjunction (AND):
If P∧Q, then P is valid.
If P∧Q, then Q is valid.
E Disjunction (OR):
If P∨Q, and [P]→R and [Q]→R, then R is valid.
E Biconditional/equivalence (↔):
If P↔Q, and P is true, then Q is valid.
If P↔Q, and Q is true, then P is valid.
E Implication (→):
If P→Q, and P is true, then Q is valid.
E Negation (NOT):
If ¬¬P, then P is valid.
E Universal quantifier (∀):
If ∀xP(x), then P(y) is valid for some independent variable y.
E Existential quantifier (∃):
If ∃xP, and [P]→Q independent of x, then Q is valid.
CONTENTS:
0:00 Introduction
1:05 Rules for Conjunction (AND)
1:31 Rules for Disjunction (OR)
1:32 What is the point? Axioms!
3:18 Example 1: Can we swap A and B?
4:50 Example 2: Deconstructing OR
5:38 Rules for Implication (IMP)
6:44 Rules for Equivalence (XNOR)
7:24 Example 3: From equivalence to implication
9:28 Rules for Negation (NOT)
10:49 Temporary Assumptions Workshop
12:06 Example 4: Creating a contradiction
14:12 Rules for Existential Quantifier (∃)
15:00 Rules for Universal Quantifier (∀)
15:28 Bound and Free Variables
17:34 Summary
17:53 Example 5: Is tiger a mammal?
20:03 Conclusion
20:21 Example 6: Every likes kiwis, Milo might like pears
24:38 Example 7: For all, A is true ⇒ For nobody, A is false
31:10 Example 8: White cars and engines
35:53 Example 9: Proving a negative?
38:51 Links

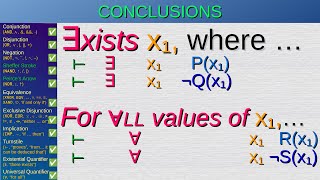







Информация по комментариям в разработке