Olá, amigos do meu canal no YouTube. Eu sou o professor Demóclis Rocha e neste vídeo apresentarei o cálculo de
3/2-1/3-1/5
Quanto que dá?
Começamos observando que essas frações têm denominadores 2, 3 e 5, isto é, os denominadores são diferentes. Assim, para calcular o valor da expressão podemos começar determinando o mmc desses denominadores, calculando o mmc de 2, 3 e 5.
Vamos executar o algoritmo da fatoração simultânea.
Para tanto, escrevemos o 2, o 3 e o 5, usando vírgulas apenas para separá-los.
Agora, testamos a divisibilidade desses números pelo primeiro número primo natural, que é o 2. Algum desses números é divisível por 2?
Sim, o 2 é divisível por 2. Quanto que dá 2 dividido por 2? Dá 1. Então, escrevemos 1 abaixo do 2.
Como 3 e 5 não são divisíveis por 2, nós apenas os repetimos.
Temos agora os números 1, 3 e 5. Nenhum deles é divisível por 2. Passamos então para o próximo número primo natural, que é o 3.
Algum desses números é divisível por 3? Sim, 3 dividido por 3 é igual a 1. Muito bem.
Como 1 não é divisível por 3, nós apenas o repetimos. Como 3 dividido por 3 é igual a 1, escrevemos 1 abaixo do 3. Como 5 não é divisível por 3, nós apenas o repetimos.
Temos agora os números 1,5 e 1. Nenhum deles é divisível por 2, nenhum deles é divisível por 3. Como o próximo número primo natural é o 5, perguntamos: algum desses números é divisível por 5?
Você vai dizer: o 5 é divisível por 5. Você tem razão: 5 dividido por 5 é igual a 1.
Vamos lá!
Como 1 não é divisível por 5, nós apenas repetimos esses dois primeiros 1’s. Como 5 dividido por 5 é igual a 1, escrevemos 1 abaixo do 5.
Essa parte acabou, pois no pé de cada coluna da esquerda apareceu o número 1.
Para calcular o mmc, basta multiplicar os números que apareceram na coluna da direita. Vamos lá!
2x3=6, guarde o 6 na memória.
6x5=30. Pronto, o mmc de 2,3 e 5 é igual a 30.
O que a gente vai fazer com esse 30? Ele será o denominador de três novas frações equivalentes às que já temos.
Por exemplo, no primeiro caso. O denominador era 2 e agora é 30. O 2 deve ser multiplicado por quanto para resultar em 30? 2x15 é igual a 30. Então para obter o numerador da fração equivalente, devemos multiplicar o 3 também por 15. Como 3x15=45, o numerador da fração equivalente é 45. Alguns professores preferem ensinar assim: 30 dividido por 2 é igual a 15 e 15 multiplicado por 3 é igual a 45. Dá no mesmo. De todo jeito, podemos dizer que 3/2 e 45/30 são frações equivalente.
Seguimos em frente fazendo o mesmo com as outras frações.
Veja. O denominador que era 3, agora é 30 na fração equivalente. O 3 deve ser multiplicado por quanto para resultar em 30? 3x10 é igual a 30. Então para obter o numerador da fração equivalente, devemos multiplicar o 1 também por 10. Como 1x10=10, o numerador da fração equivalente é 10. Alguns professores preferem ensinar assim: 30 dividido por 3 é igual a 10 e 10 multiplicado por 1 é igual a 10. Dá no mesmo. De todo jeito, podemos dizer que 1/3 e 10/30 são frações equivalentes.
Continuando. O denominador que era 5, agora é 30 na fração equivalente. O 5 deve ser multiplicado por quanto para resultar em 30? 5x6 é igual a 30. Então para obter o numerador da fração equivalente, devemos multiplicar o 1 também por 6. Como 1x6=6, o numerador da fração equivalente é 6. Alguns professores preferem ensinar assim: 30 dividido por 5 é igual a 6 e 6 multiplicado por 1 é igual a 6. Dá no mesmo. De todo jeito, podemos dizer que 1/5 e 6/30 são frações equivalentes.
Agora, em vez de operar diretamente com frações que têm denominadores diferentes, operamos com frações equivalente, mas que têm denominadores iguais. Aí fica fácil. Basta repetir o denominador e fazer as continhas com os numeradores para obter o resultado.
Vamos lá!
45 – 10 =35 e 35-6 =29
Repetimos o denominador e temos o resultado, que é a fração 29/30.
Se você gostou, clique em gostei!
Deixe um comentário sobre o vídeo! Ele te ajudou? Diga aí!
Se o vídeo te ajudou, compartilhe com seus colegas!
Um abraço e até a próxima, tchau!
Playlist sobre frações:
• FRAÇÕES






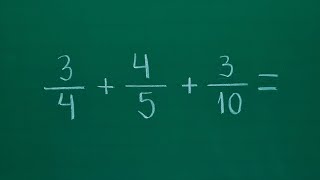



Информация по комментариям в разработке