There are many reasons you could call this the most beautiful equation in mathematics. However, personally, this equation is astounding because it links so many aspects in maths in ways that might not seem related at all at the first glance. We have the Taylor series, the Euler constant, the famous Greek alphabet pi, the trigonometric functions sine and cosine, and also, perhaps a bit more surprisingly, the imaginary unit i. In many ways, this could be considered as an important link between the real and imaginary world in maths, and how maybe the imaginary unit is not that imaginary after all….
This video was made in collaboration with @merlinomath. Make sure to check him out for some great animations too and the Spanish version of this video.
Finally, remember to leave a like on the video, and follow the channel if you haven’t already!
Here is the transcript:
"There's a certain magic in mathematics, a magic that connects the abstract to the real, the imaginary to the tangible. Among the countless equations that define our universe, there's one that stands out for its elegance and simplicity. This is Euler's Identity.
Imagine a journey that begins with a point, traveling along a path that curves and winds through the fabric of reality. Each step along this path reveals a deeper connection, a hidden truth that links the seen and the unseen, the known and the unknown.
At the heart of this journey is Leonhard Euler, a soul whose boundless curiosity illuminated the world.
His gift to us is the constant e, regarded as the second most influential number in all of mathematics.
The full beauty of Euler's Identity emerges through the Taylor Series, which deconstructs complex functions into infinite sums of simpler terms- namely polynomials.
This is the Taylor series for e^x. Let’s dive into the complex world. I will substitute ix in place of x, and we will end up getting the Taylor expansion of e to the ix. Notice something interesting, as the left side forms the Taylor series for cosine of X, and the right side forms the Taylor expansion for I times sine of x.
We can now write e^ix as cosx +I sine x. Now, simply substituting pi for x will gives us the following expression, and we get e to the I pi= -1.
But what this expression is really saying is that we can think of e^ I alpha as a complex number with trigonometric coordinates, namely cos alpha and I sine alpha.
And that brings us inevitably to a whole new algebraic structure where all the possible values of e^inPi lie in a circle. A complex circle
However, this expression also needs to align with this result. Do you remember the expression we introduced at the beginning? That's the e number limit expression, from there we extend it for any power of x and the question now is what happens when we plug i into?
In other words, What happens when x = Pi?. Let's imagine that we have no idea. A very simple thing we can do is to try substituting some values of n and calculate their different complex values. I know it seems intimidating, but in the end, it is just a simple complex number that can be represented on a complex plane.
If we continue this process as n tends to infinity, surprisingly, we can observe that the values converge to −1.
But this is not a proof at all; it is just an intuition
In order to prove this, we will split the path into partitions, and show that the powers of the expression converge to -1, as the number of partitions goes to infinity.
For example, for n=1n = 1n=1 we have 1 possibility, for n=2n = 2n=2 we have 2 possible partitions. Notice that the height decreases and that these two numbers are consecutive multiplications.
And that leads us to a beautiful proof, where the path eventually converges to a half a circle with radius=1
And that leaves with a final question, what happens when we plug into the expression x=2PI instead.
And what we find is even more surprising and just beautiful. That the notion of the complex numbers lies in a circular structure.
So again , we come back to the same idea and that is truly remarkable, and probably the most beautiful proof in Mathematics

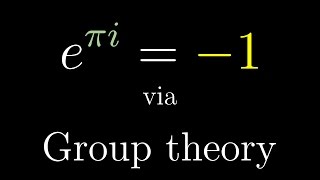







Информация по комментариям в разработке